Baekjoon 6549
히스토그램에서 가장 큰 직사각형
QUESTION ❔
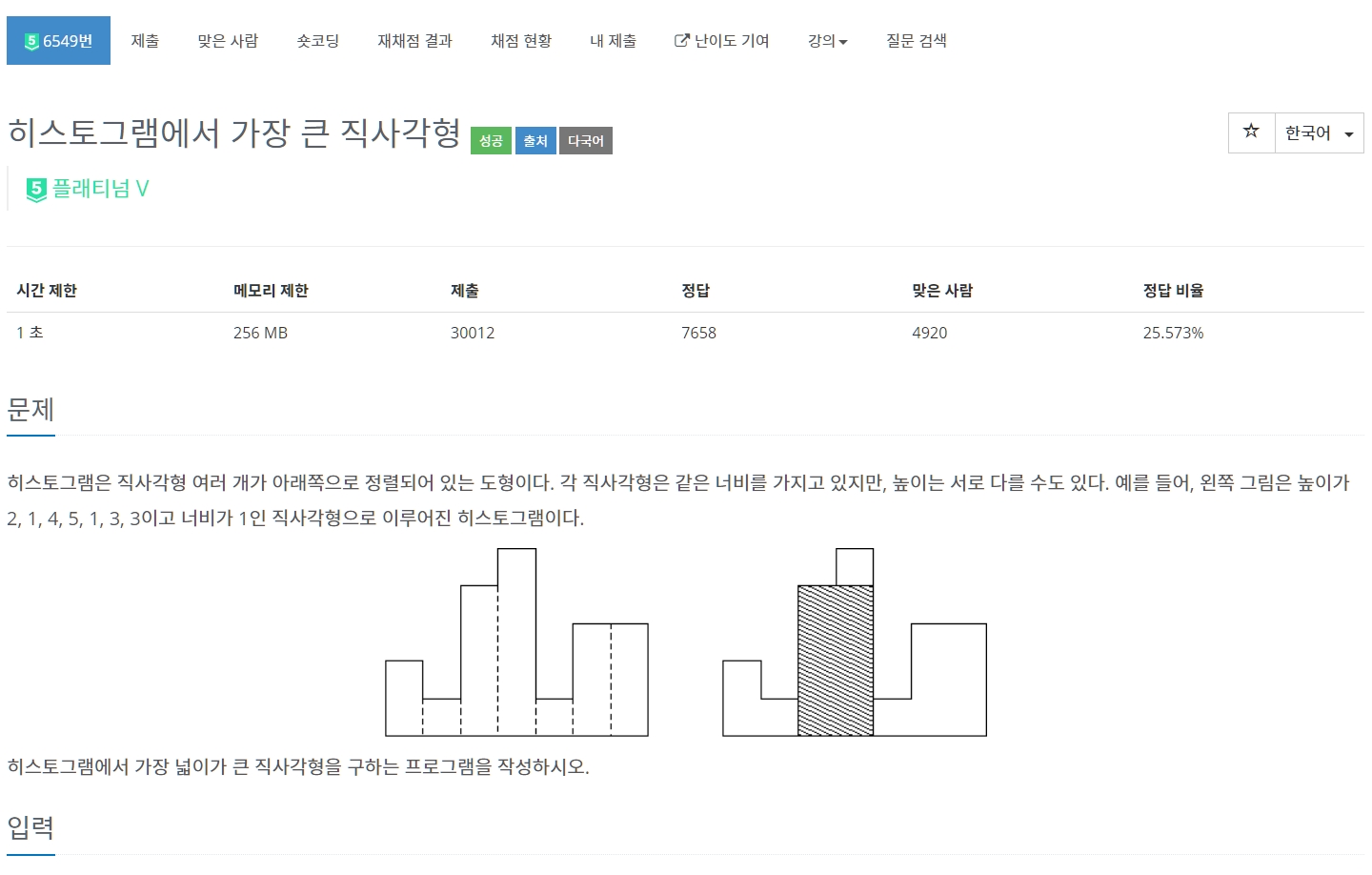
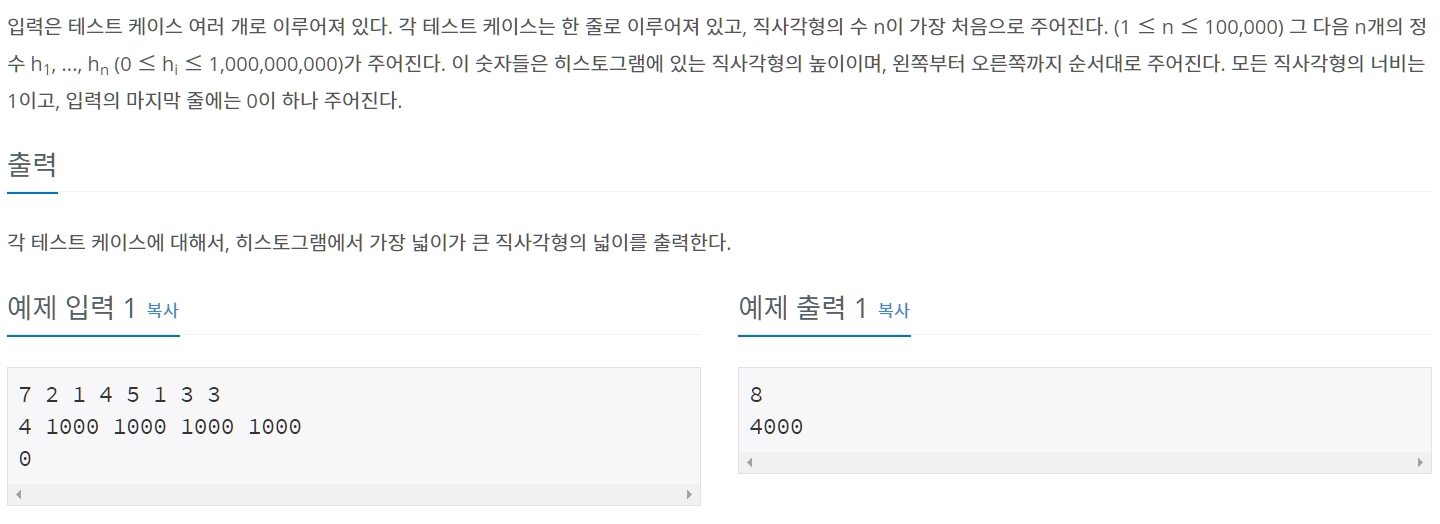
CODE ⌨️
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
int n;
vector<int> arr;
vector<int> tree;
vector<ll> ans;
void make_SegmentTree(int node, int start, int end)
{
if (start == end)
{
tree[node] = start;
return;
}
int mid = (start + end) / 2;
make_SegmentTree(node * 2, start, mid);
make_SegmentTree(node * 2 + 1, mid + 1, end);
if (arr[tree[node * 2]] <= arr[tree[node * 2 + 1]]) tree[node] = tree[node * 2];
else tree[node] = tree[node * 2 + 1];
}
int find_idx(int node, int start, int end, int l, int r)
{
if (l > end || r < start) return -1;
if (l <= start && end <= r) return tree[node];
int mid = (start + end) / 2;
int l_idx = find_idx(node * 2, start, mid, l, r);
int r_idx = find_idx(node * 2 + 1, mid + 1, end, l, r);
if (l_idx == -1) return r_idx;
else if (r_idx == -1) return l_idx;
else if (arr[l_idx] <= arr[r_idx]) return l_idx;
else return r_idx;
}
ll find_max(int start, int end)
{
int idx = find_idx(1, 0, n - 1, start, end);
ll result = (ll)(end - start + 1) * (ll)arr[idx];
if (start <= idx - 1)
{
ll l_result = find_max(start, idx - 1);
result = max(result, l_result);
}
if (idx + 1 <= end)
{
ll r_result = find_max(idx + 1, end);
result = max(result, r_result);
}
return result;
}
void solve()
{
int tree_ht = (int)ceil(log2(n));
int tree_sz = pow(2, tree_ht + 1);
tree.resize(tree_sz);
make_SegmentTree(1, 0, n - 1);
ll result = find_max(0, n - 1);
ans.push_back(result);
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
while (cin >> n)
{
if (n == 0) break;
tree.clear();
arr.clear();
for (int i = 0; i < n; i++)
{
int a;
cin >> a;
arr.push_back(a);
}
solve();
}
for (int i = 0; i < ans.size(); i++)
{
cout << ans[i] << "\n";
}
return 0;
}
RESULT 💛

SIMPLE DISCUSSION ✏️
세그먼트 트리 관련 문제였다.
SOURCE 💎
Baekjoon_Link 👈 Click here
*****
NOT A TALENT ❎ NOT GIVING UP ✅
CopyRight ⓒ 2022 DCherish All Rights Reserved.
CopyRight ⓒ 2022 DCherish All Rights Reserved.